|
Parte Nona
Applicazioni di statistica
meteorologica
Applichiamo ancora il metodo dei minimi quadrati
alla caduta annua di neve fresca a Genova.
Esiste a questo riguardo, una serie di
osservazioni giornaliere che si sono protratte con continuità per
124 anni, dal 1870 al 1993, presso l’osservatorio meteorologico
dell’università di Genova, in via Balbi. Bisogna subito dire che la
valutazione della neve fresca caduta durante una nevicata si presta
ad una non trascurabile ambiguità. Secondo prescrizioni attuali la
misura dovrebbe essere effettuata, su una opportuna superficie
orizzontale, da una a quattro volte al giorno (National Weather
Service – USA) tenendo conto e sommando i valori massimi
dell’altezza raggiunta dalla neve fresca caduta nei vari intervalli
di tempo. Rispetto a uno standard di due misurazioni al giorno così
eseguite, per Torino si sono ipotizzate sottostime sino al 12% per
una sola misura giornaliera ad una data predeterminata od alla fine
della nevicata (cf. Gennaro di Napoli e Luca Mercalli :il Clima di
Torino, Torino 2008) . Ancora, alla stazione meteo amatoriale di
Gardolo - Trento, si è verificato per le ultime sette nevicate
annuali uno scostamento sino al 17% tra le misure dei valori massimi
effettuate 4 volte al giorno rispetto a quelle effettuate, sempre
tenendo conto dei valori massimi, una sola volta. In particolare per
Genova è pure oltremodo importante considerare l’influenza del vento
che può incrementare o ridurre enormemente gli accumuli misurati, ed
il vento accompagna gran parte delle nevicate genovesi, nevicate che
si presentano talora sotto forma di vera e propria tormenta.
Con queste cautele e con le relative incertezze
sulle metodologie di misura adottate nel passato, incertezze che
dovrebbero poter essere ridotte da un più approfondito esame dei
dati, riportiamo nella tabella sottostante i valori annuali ( per
anno civile), arrotondati al cm, come scaturiscono da una prima
indagine sui registri storici delle osservazioni.
|
Anno |
Neve
caduta |
Anno |
Neve
caduta |
Anno |
Neve
caduta |
Anno |
Neve
caduta |
|
|
|
|
|
|
|
|
|
|
1870 |
55 |
1904 |
0 |
1938 |
26 |
1972 |
14 |
|
1871 |
1 |
1905 |
24 |
1939 |
0 |
1973 |
0 |
|
1872 |
0 |
1906 |
7 |
1940 |
1 |
1974 |
0 |
|
1873 |
0 |
1907 |
20 |
1941 |
11 |
1975 |
0 |
|
1874 |
3 |
1908 |
0 |
1942 |
2 |
1976 |
7 |
|
1875 |
35 |
1909 |
59 |
1943 |
0 |
1977 |
0 |
|
1876 |
8 |
1910 |
0 |
1944 |
8 |
1978 |
17 |
|
1877 |
0 |
1911 |
9 |
1945 |
26 |
1979 |
10 |
|
1878 |
21 |
1912 |
14 |
1946 |
25 |
1980 |
5 |
|
1879 |
35 |
1913 |
0 |
1947 |
37 |
1981 |
16 |
|
1880 |
15 |
1914 |
18 |
1948 |
5 |
1982 |
0 |
|
1881 |
15 |
1915 |
28 |
1949 |
3 |
1983 |
0 |
|
1882 |
0 |
1916 |
0 |
1950 |
14 |
1984 |
0 |
|
1883 |
23 |
1917 |
10 |
1951 |
0 |
1985 |
37 |
|
1884 |
0 |
1918 |
0 |
1952 |
0 |
1986 |
29 |
|
1885 |
0 |
1919 |
0 |
1953 |
0 |
1987 |
7 |
|
1886 |
38 |
1920 |
7 |
1954 |
18 |
1988 |
0 |
|
1887 |
65 |
1921 |
0 |
1955 |
4 |
1989 |
0 |
|
1888 |
2 |
1922 |
2 |
1956 |
42 |
1990 |
0 |
|
1889 |
1 |
1923 |
0 |
1957 |
0 |
1991 |
11 |
|
1890 |
4 |
1924 |
0 |
1958 |
8 |
1992 |
0 |
|
1891 |
0 |
1925 |
1 |
1959 |
0 |
1993 |
0 |
|
1892 |
12 |
1926 |
23 |
1960 |
6 |
1994 |
|
|
1893 |
50 |
1927 |
2 |
1961 |
0 |
1995 |
|
|
1894 |
0 |
1928 |
17 |
1962 |
2 |
1996 |
|
|
1895 |
37 |
1929 |
16 |
1963 |
13 |
1997 |
|
|
1896 |
1 |
1930 |
0 |
1964 |
0 |
1998 |
|
|
1897 |
0 |
1931 |
0 |
1965 |
5 |
1999 |
|
|
1898 |
0 |
1932 |
23 |
1966 |
0 |
2000 |
|
|
1899 |
8 |
1933 |
22 |
1967 |
13 |
2001 |
|
|
1900 |
0 |
1934 |
0 |
1968 |
0 |
2002 |
|
|
1901 |
17 |
1935 |
10 |
1969 |
7 |
2003 |
|
|
1902 |
5 |
1936 |
0 |
1970 |
7 |
2004 |
|
|
1903 |
0 |
1937 |
0 |
1971 |
9 |
2005 |
|
Tab.1 Caduta di neve
fresca a Genova – Osservatorio di via Balbi
Da tali dati otteniamo:
|
| numero dei valori |
: 124 |
| valore medio |
: 9,8 cm |
| valore minimo |
: 0 cm |
| valore max |
: 65 cm |
| mediana |
: 3,5 cm |
| dev. standard |
: 13,8 cm |
| dev. standard % |
: 140 |
| percentile 0,5 |
: 3,5 cm |
| percentile 0,9 |
: 27,4 cm |
| percentile 0,99 |
: 65 cm |
L’andamento delle cadute di neve è rappresentato
dai grafici di Fig.1
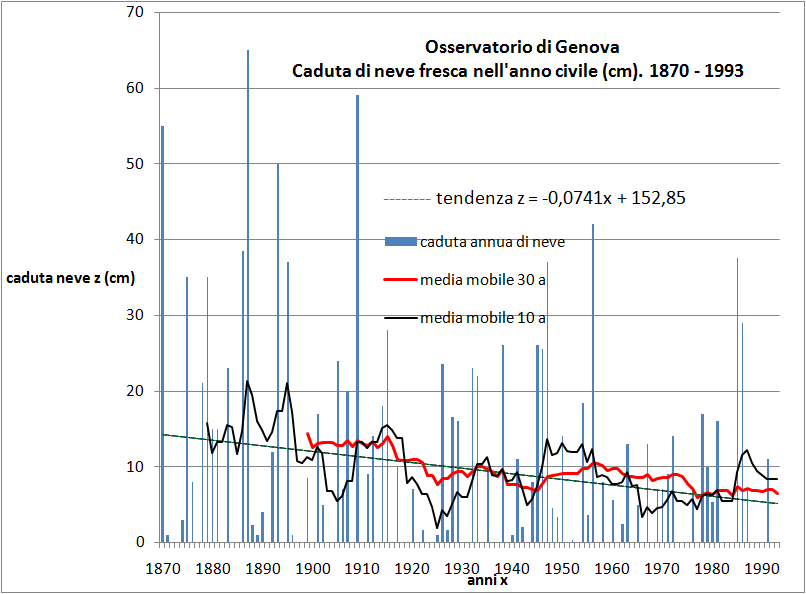
Fig.1 - Caduta di neve a
Genova (via Balbi). 1870 -1993
Utilizzando il metodo dei minimi quadrati si può
ottenere la retta interpolatrice riportata:
1) z =
Bx+A
Abbiamo:
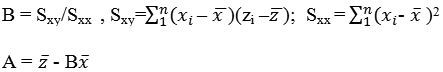
Avendo indicato con
xi ed
zi risp. gli
anni e le altezze della neve caduta nell’anno
i e con
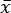ed
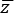le rispettive medie.
Otteniamo:
Sxx
= 158906
Sxz = 11767,6
A = 152,8
B = -0,074
Da cui:
2) z =
-0,074x + 152,8
E’ evidente il calo secolare della caduta di
neve, pressoché dimezzatasi in 124 anni a far fede alla curva
interpolatrice. La tendenza è confermata anche dalle medie mobili di
10 e 30 anni riportate nello stesso grafico. Ricordiamo che la media
mobile di ordine m
indica, all’anno n,
la media degli m
anni precedenti lo stesso anno
n.
Ritorniamo ora alla formula di Gumbel detta anche
estrema di tipo 1 proposta, ad essere rigorosi, per valutare tempi
di ritorno di fenomeni meteo estremi quali ad es. la massima
precipitazione in un giorno o la massima portata di un corso d’acqua
nel corso di determinato numero di anni, ed applichiamola alle
nevicate annuali a Genova. Nella tabella 2 sono riportate: le cadute
misurate annuali di neve z
nell’ ordine decrescente m,
la durata o probabilità di non superamento data da
(1-p) = m/(n+1),
con n = 124 =
numero delle osservazioni, il tempo di ritorno
TR cioè il tempo che si
può ritenere ricorra perché un evento di grandezza uguale o
superiore si ripresenti = 1/p,
la variabile ridotta di Gumbel
y, la caduta teorica di neve prevista
zG, la
stessa grandezza depennata dai valori negativi
zcorr .
Ordine
m |
Caduta neve
z cm |
Durata
(1-p) |
Tempo
TR |
y |
z
G. |
zG
corr |
|
1 |
0 |
0,008 |
1,01 |
-1,57 |
-13,4 |
0 |
|
2 |
0 |
0,016 |
1,02 |
-1,42 |
-11,7 |
0 |
|
3 |
0 |
0,024 |
1,02 |
-1,32 |
-10,6 |
0 |
|
4 |
0 |
0,032 |
1,03 |
-1,24 |
-9,7 |
0 |
|
5 |
0 |
0,04 |
1,04 |
-1,17 |
-9,0 |
0 |
|
6 |
0 |
0,048 |
1,05 |
-1,11 |
-8,4 |
0 |
|
7 |
0 |
0,056 |
1,06 |
-1,06 |
-7,8 |
0 |
|
8 |
0 |
0,064 |
1,07 |
-1,01 |
-7,3 |
0 |
|
9 |
0 |
0,072 |
1,08 |
-0,97 |
-6,8 |
0 |
|
10 |
0 |
0,08 |
1,09 |
-0,93 |
-6,4 |
0 |
|
11 |
0 |
0,088 |
1,10 |
-0,89 |
-6,0 |
0 |
|
12 |
0 |
0,096 |
1,11 |
-0,85 |
-5,6 |
0 |
|
13 |
0 |
0,104 |
1,12 |
-0,82 |
-5,2 |
0 |
|
14 |
0 |
0,112 |
1,13 |
-0,78 |
-4,8 |
0 |
|
15 |
0 |
0,12 |
1,14 |
-0,75 |
-4,5 |
0 |
|
16 |
0 |
0,128 |
1,15 |
-0,72 |
-4,2 |
0 |
|
17 |
0 |
0,136 |
1,16 |
-0,69 |
-3,8 |
0 |
|
18 |
0 |
0,144 |
1,17 |
-0,66 |
-3,5 |
0 |
|
19 |
0 |
0,152 |
1,18 |
-0,63 |
-3,2 |
0 |
|
20 |
0 |
0,16 |
1,19 |
-0,61 |
-2,9 |
0 |
|
21 |
0 |
0,168 |
1,20 |
-0,58 |
-2,6 |
0 |
|
22 |
0 |
0,176 |
1,21 |
-0,55 |
-2,4 |
0 |
|
23 |
0 |
0,184 |
1,23 |
-0,53 |
-2,1 |
0 |
|
24 |
0 |
0,192 |
1,24 |
-0,50 |
-1,8 |
0 |
|
25 |
0 |
0,2 |
1,25 |
-0,48 |
-1,5 |
0 |
|
26 |
0 |
0,208 |
1,26 |
-0,45 |
-1,3 |
0 |
|
27 |
0 |
0,216 |
1,28 |
-0,43 |
-1,0 |
0 |
|
28 |
0 |
0,224 |
1,29 |
-0,40 |
-0,7 |
0 |
|
29 |
0 |
0,232 |
1,30 |
-0,38 |
-0,5 |
0 |
|
30 |
0 |
0,24 |
1,32 |
-0,36 |
-0,2 |
0 |
|
31 |
0 |
0,248 |
1,33 |
-0,33 |
0,0 |
0,0 |
|
32 |
0 |
0,256 |
1,34 |
-0,31 |
0,3 |
0,3 |
|
33 |
0 |
0,264 |
1,36 |
-0,29 |
0,5 |
0,5 |
|
34 |
0 |
0,272 |
1,37 |
-0,26 |
0,7 |
0,7 |
|
35 |
0 |
0,28 |
1,39 |
-0,24 |
1,0 |
1,0 |
|
36 |
0 |
0,288 |
1,40 |
-0,22 |
1,2 |
1,2 |
|
37 |
0 |
0,296 |
1,42 |
-0,20 |
1,5 |
1,5 |
|
38 |
0 |
0,304 |
1,44 |
-0,17 |
1,7 |
1,7 |
|
39 |
0 |
0,312 |
1,45 |
-0,15 |
1,9 |
1,9 |
|
40 |
0 |
0,32 |
1,47 |
-0,13 |
2,2 |
2,2 |
|
41 |
0 |
0,328 |
1,49 |
-0,11 |
2,4 |
2,4 |
|
42 |
0 |
0,336 |
1,51 |
-0,09 |
2,7 |
2,7 |
|
43 |
0 |
0,344 |
1,52 |
-0,06 |
2,9 |
2,9 |
|
44 |
0 |
0,352 |
1,54 |
-0,04 |
3,1 |
3,1 |
|
45 |
0 |
0,36 |
1,56 |
-0,02 |
3,4 |
3,4 |
|
46 |
0 |
0,368 |
1,58 |
0,00 |
3,6 |
3,6 |
|
47 |
0 |
0,376 |
1,60 |
0,02 |
3,8 |
3,8 |
|
48 |
0 |
0,384 |
1,62 |
0,04 |
4,1 |
4,1 |
|
49 |
0,1 |
0,392 |
1,64 |
0,07 |
4,3 |
4,3 |
|
50 |
0,3 |
0,4 |
1,67 |
0,09 |
4,5 |
4,5 |
|
51 |
1 |
0,408 |
1,69 |
0,11 |
4,8 |
4,8 |
|
52 |
1 |
0,416 |
1,71 |
0,13 |
5,0 |
5,0 |
|
53 |
1 |
0,424 |
1,74 |
0,15 |
5,2 |
5,2 |
|
54 |
1 |
0,432 |
1,76 |
0,18 |
5,5 |
5,5 |
|
55 |
1,3 |
0,44 |
1,79 |
0,20 |
5,7 |
5,7 |
|
56 |
1,6 |
0,448 |
1,81 |
0,22 |
6,0 |
6,0 |
|
57 |
1,7 |
0,456 |
1,84 |
0,24 |
6,2 |
6,2 |
|
58 |
2 |
0,464 |
1,87 |
0,26 |
6,4 |
6,4 |
|
59 |
2,3 |
0,472 |
1,89 |
0,29 |
6,7 |
6,7 |
|
60 |
2,5 |
0,48 |
1,92 |
0,31 |
6,9 |
6,9 |
|
61 |
3 |
0,488 |
1,95 |
0,33 |
7,2 |
7,2 |
|
62 |
3,4 |
0,496 |
1,98 |
0,35 |
7,4 |
7,4 |
|
63 |
3,6 |
0,504 |
2,02 |
0,38 |
7,7 |
7,7 |
|
64 |
4 |
0,512 |
2,05 |
0,40 |
7,9 |
7,9 |
|
65 |
4,6 |
0,52 |
2,08 |
0,42 |
8,2 |
8,2 |
|
66 |
5 |
0,528 |
2,12 |
0,45 |
8,4 |
8,4 |
|
67 |
5 |
0,536 |
2,16 |
0,47 |
8,7 |
8,7 |
|
68 |
5,3 |
0,544 |
2,19 |
0,50 |
8,9 |
8,9 |
|
69 |
5,4 |
0,552 |
2,23 |
0,52 |
9,2 |
9,2 |
|
70 |
7 |
0,56 |
2,27 |
0,55 |
9,5 |
9,5 |
|
71 |
7 |
0,568 |
2,31 |
0,57 |
9,7 |
9,7 |
|
72 |
7 |
0,576 |
2,36 |
0,59 |
10,0 |
10,0 |
|
73 |
7 |
0,584 |
2,40 |
0,62 |
10,3 |
10,3 |
|
74 |
7 |
0,592 |
2,45 |
0,65 |
10,5 |
10,5 |
|
75 |
8 |
0,6 |
2,50 |
0,67 |
10,8 |
10,8 |
|
76 |
8 |
0,608 |
2,55 |
0,70 |
11,1 |
11,1 |
|
77 |
8 |
0,616 |
2,60 |
0,72 |
11,4 |
11,4 |
|
78 |
8,5 |
0,624 |
2,66 |
0,75 |
11,7 |
11,7 |
|
79 |
9 |
0,632 |
2,72 |
0,78 |
12,0 |
12,0 |
|
80 |
9 |
0,64 |
2,78 |
0,81 |
12,3 |
12,3 |
|
81 |
10 |
0,648 |
2,84 |
0,84 |
12,6 |
12,6 |
|
82 |
10 |
0,656 |
2,91 |
0,86 |
12,9 |
12,9 |
|
83 |
10 |
0,664 |
2,98 |
0,89 |
13,2 |
13,2 |
|
84 |
11 |
0,672 |
3,05 |
0,92 |
13,5 |
13,5 |
|
85 |
11 |
0,68 |
3,13 |
0,95 |
13,8 |
13,8 |
|
86 |
12 |
0,688 |
3,21 |
0,98 |
14,2 |
14,2 |
|
87 |
12 |
0,696 |
3,29 |
1,01 |
14,5 |
14,5 |
|
88 |
13 |
0,704 |
3,38 |
1,05 |
14,9 |
14,9 |
|
89 |
13 |
0,712 |
3,47 |
1,08 |
15,2 |
15,2 |
|
90 |
14 |
0,72 |
3,57 |
1,11 |
15,6 |
15,6 |
|
91 |
14 |
0,728 |
3,68 |
1,15 |
15,9 |
15,9 |
|
92 |
14 |
0,736 |
3,79 |
1,18 |
16,3 |
16,3 |
|
93 |
15 |
0,744 |
3,91 |
1,22 |
16,7 |
16,7 |
|
94 |
15 |
0,752 |
4,03 |
1,26 |
17,1 |
17,1 |
|
95 |
16 |
0,76 |
4,17 |
1,29 |
17,5 |
17,5 |
|
96 |
16 |
0,768 |
4,31 |
1,33 |
17,9 |
17,9 |
|
97 |
16,6 |
0,776 |
4,46 |
1,37 |
18,4 |
18,4 |
|
98 |
17 |
0,784 |
4,63 |
1,41 |
18,8 |
18,8 |
|
99 |
17 |
0,792 |
4,81 |
1,46 |
19,3 |
19,3 |
|
100 |
18 |
0,8 |
5,00 |
1,50 |
19,7 |
19,7 |
|
101 |
18,4 |
0,808 |
5,21 |
1,55 |
20,2 |
20,2 |
|
102 |
20 |
0,816 |
5,43 |
1,59 |
20,7 |
20,7 |
|
103 |
21 |
0,824 |
5,68 |
1,64 |
21,3 |
21,3 |
|
104 |
22 |
0,832 |
5,95 |
1,69 |
21,8 |
21,8 |
|
105 |
23 |
0,84 |
6,25 |
1,75 |
22,4 |
22,4 |
|
106 |
23 |
0,848 |
6,58 |
1,80 |
23,0 |
23,0 |
|
107 |
23 |
0,856 |
6,94 |
1,86 |
23,6 |
23,6 |
|
108 |
24 |
0,864 |
7,35 |
1,92 |
24,3 |
24,3 |
|
109 |
25,5 |
0,872 |
7,81 |
1,99 |
25,0 |
25,0 |
|
110 |
26 |
0,88 |
8,33 |
2,06 |
25,7 |
25,7 |
|
111 |
26 |
0,888 |
8,93 |
2,13 |
26,5 |
26,5 |
|
112 |
28 |
0,896 |
9,62 |
2,21 |
27,4 |
27,4 |
|
113 |
29 |
0,904 |
10,42 |
2,29 |
28,3 |
28,3 |
|
114 |
35 |
0,912 |
11,36 |
2,38 |
29,3 |
29,3 |
|
115 |
35 |
0,92 |
12,50 |
2,48 |
30,3 |
30,3 |
|
116 |
37 |
0,928 |
13,89 |
2,59 |
31,5 |
31,5 |
|
117 |
37 |
0,936 |
15,63 |
2,72 |
32,8 |
32,8 |
|
118 |
37,5 |
0,944 |
17,86 |
2,85 |
34,3 |
34,3 |
|
119 |
38,5 |
0,952 |
20,83 |
3,01 |
36,0 |
36,0 |
|
120 |
42 |
0,96 |
25,00 |
3,20 |
38,0 |
38,0 |
|
121 |
50 |
0,968 |
31,25 |
3,43 |
40,5 |
40,5 |
|
122 |
55 |
0,976 |
41,67 |
3,72 |
43,6 |
43,6 |
|
123 |
59 |
0,984 |
62,50 |
4,13 |
48,0 |
48,0 |
|
124 |
65 |
0,992 |
125,00 |
4,82 |
55,5 |
55,5 |
Tab. 2 Analisi di Gumbel
delle cadute di neve a Genova
La variabile ridotta di Gumbel
y è legata alla durata
o probabilità di non superamento
1-p e dunque al tempo
di ritorno TR da :
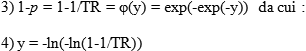
A sua volta secondo Gumbel
y risulta funzione
lineare di z attraverso
le caratteristiche della statistica: media
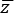e scarto quadratico medio
 :
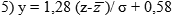
Segue che:
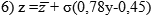
Con i nostri dati abbiamo così:
7)
z =9,8 +13,8(0,78z-0,45)
Ne scaturiscono i grafici riportati nella Fig.
2. Buona è la corrispondenza tra i valori misurati e quelli
previsti sino ad un tempo di ritorno di ca.20 anni, poi
significativa sottostima della retta di Gumbel. Al contrario
l’interpolazione lineare dei dati misurati porge una retta che viene
quasi a coincidere con essa e non è qui evidenziata. Al suo posto è
riportata la curva interpolatrice di terzo grado anch’essa
ricavabile col metodo dei minimi quadrati cioè minimizzando
l’espressione:
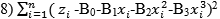
per determinare i coefficienti
B. Essa pare
adattarsi abbastanza bene ai valori misurati
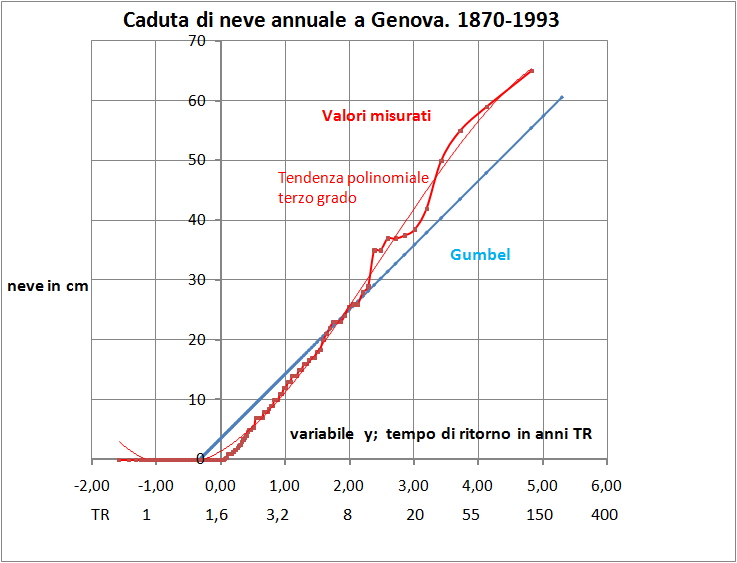
Fig. 2 - Caduta
di neve a Genova (via Balbi). Anni 1870-1993. Valori
misurati e previsti |
