

|
di: Diego Rosa |
Stabilità instabilità atmosferica
Parte ottava
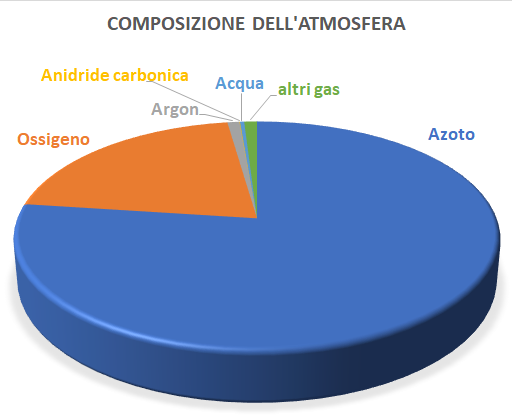 Fig 1 - Composizione dell'atmosfera
Fig 1 - Composizione dell'atmosfera
1. L'atmosfera terrestre
Fino all’altezza di ca. 80-100 km l’atmosfera terrestre ha una composizione chimica pressoché costante. In termini di composizione molare abbiamo:
-Azoto N2 = 78%
-Ossigeno O2 = 20,9%
-Argon Ar = 0,938 %
-Anidride carbonica CO2 = 0,04% ca
-Acqua H2O = dal 5 % al 7/% a 40C°; 0,5% a = 0 C°
-Altri gas < del’ 1%
L’equazione dei gas perfetti.
1) PV = RT
riferita ad un grammo-mole di gas con R = 8,31 g/(mole K) diventa per 1 Kg di sostanza su 1 m3
PdV = 8,31 *1000/28,96 *T = RdT = 286,94 *T ( J/(Kg) *K) per 1 Kg di aria secca su 1 m3
e rispettivamente:
PvV = 8,31 *1000/18 *T = RvT = 461*T (J /(Kg )*K) per 1 Kg di vapore d’acqua su 1 m3
L’ umidità specifica q è definita come massa di vapore mv per massa d’aria m:
q = mv/m
mentre il rapporto di mescolamento come massa di vapore mv su massa d’aria secca md
r = mv/md
Tenendo conto che mv « md dalla relazione dei gas perfetti che coinvolge Il rapporto η= Rd /Rv si ha per la pressione del vapore Pv indicando con P la pressione totale dell’aria:
2) Pv ≈ Pr/ η ≈ Pq/ η
L’umidità relativa è definita dal rapporto tra la massa del vapore presente e quella del vapore saturo alla stessa temperatura:
U = mv/mw = Pv/Pw ≈ q/qw ≈ r/rw
espresso in percentuale.
La temperatura di rugiada la pressione di vapore è pari a quella di saturazione.
2. Espansione adiabatica secca
I movimenti ascensionali dell’atmosfera sono i motori principali delle precipitazioni.
saminiamo il caso dell’espansione dell’aria durante la quale non vi sia condensazione del vapore contenuto, né scambi di calore con le masse d’aria circostanti: l’espansione adiabatica secca.
l primo principio della termodinamica porge per unità di massa.
3) δQ = CvdT +PdV
con Cv = calore specifico a volume costante, Q, = calore assorbito, T temperatura p = pressione, V= volume specifico (per unità di massa)Abbiamo ancora dall’equazione dei gas perfetti: PV = RT, R = costante, che differenziando porge:
PdV+VdP = RdT, PdV=RdT-VdP
Con R costante dei gas perfetti.
Sostituendo nella 3) otteniamo:
4) δQ=(Cv+R)dT-VdP = CP dT- VdP
Abbiamo, ponendo dP = 0: Cv +R= Cp (calore specifico a pressione costante), sostituendo V =RT/P e ponendo δQ=0:
5) (Cp-Cv) / Cp (dP/P) = dT/T
Equazione subito integrabile che porge l’equazione di Poisson:
6) T/T0= (P/P0) χ
Con χ = (CP-Cv) / CP = 0,286 per l’aria secca
Dalla 6) si suole introdurre il concetto di temperatura potenziale Ɵ:
7) Ɵ = T(1000/P) χ
Temperatura che assumerebbe una massa d’aria secca di temperatura T portata adiabaticamente alla pressione standard di 1000 hPa
3) Espansione adiabatica umida
Nel caso di espansione di aria satura si ha che dQ è diverso da 0 e pari al valore dovuto alla condensazione del vapore saturo:
si ha:
8) dQ = -Ldws
dove L è il calore di vaporizzazione,
ws è la variazione del contenuto di vapore per unita di massa d’aria.
Si ha così, per unita’di massa
9) CP dT- VdP = -Ldws
Trascurando l a variazione della quantità ws al variare della pressione dell’aria, si ottiene:
10) CP dT- VdP = -L (δws/δT) dT
Ora abbiamo che VdP= gdz con g = accelerazione di gravità e dz aumento differenziale della quota altimetrica e la 10) diventa:
11) (Cp +L δws/δT)dT= -gdz
Dividendo per CP ed essendo g/CP = dT/dz si ha:
12) (1+L/CP* δws/δT)dT= - Γd dz
Con Γd = gradiente termico in aria secca
Si ha così:
13) dT/dz = -Γd/ (1+L/CP* δws/δT) = Γs
In aria satura e in valore assoluto
14) dT/dz= Γs< Γd
La temperatura diminuisce meno, aumentando la quota, lungo una pseudo adiabatica umida che lungo una secca a causa del rilascio del calore latente di condensazione.
