 |
 |
 |
|
|
|
|
Temperatura, température, temperature, temperatur
Definizione La temperatura può definirsi come una grandezza fisica misurata dai termometri che connota la capacità dei corpi di produrre, nell’esperienza quotidiana, sensazioni di caldo o di freddo e implicitamente il verso del passaggio del calore da un corpo all’altro. Ancora fissata una scala cui riferire le indicazioni dei termometri, si può definire temperatura di un corpo come quella grandezza misurata dai suddetti termometri che si trovino in equilibrio termico con esso. La scala più comunemente usata è quella centigrada Celsius) dove il valore 0 ed il valore 100 corrispondono rispettivamente alle temperature del ghiaccio fondente (punto triplo) e dell’acqua bollente alla pressione atmosferica. Un grado centigrado, 1°C, corrisponde alla centesima parte di questo intervallo di misura, ipotizzando che la lettura sia lineare con la grandezza misurata.Tale ipotesi è assunta essere abbastanza soddisfatta riferendosi ad esempio alla proprietà di certi corpi di dilatarsi all’aumentare della temperatura e misurando tale dilatazione. La scala Fahrenheit (ancora usata negli Stati Uniti) fa corrispondere la misura in gradi °F (t(°F)) a quella in gradi °C (t(°F) ) attraverso la relazione 1) t (°F) = 32+9/5 t (°C) I primi termometri sono stati realizzati da Galileo. Temperatura assoluta e suo significato termodinamico Fondamentali esperienze ed elaborazioni teoriche del 19° secolo hanno portato a questa conclusione fondamentale: la temperatura di un corpo è espressione di quella parte della sua energia interna specifica, cioè di energia riferita all’unità di massa, che è dovuta all’agitazione termica delle molecole che lo compongono. Il calore scambiato non è altro che scambio di energia termica di agitazione molecolare da un corpo all’altro. Vale la fondamentale relazione:
2)
Cioè, il calore scambiato
(assorbito se >0), Se il lavoro è nullo e non vi è
mutazione di fase o di composizione chimica, si ha che L’esistenza di una scala assoluta delle temperature scaturisce dalle considerazioni seguenti Comportamento dei gas perfetti La pressione , la temperatura ed il volume di una mole di gas (cioè di una massa di gas pari alla sua massa molecolare espressa in g) alle condizioni ordinarie, soddisfano con buona approssimazione all’equazione dei gas perfetti: 3) p VM = C f(t) Dove p è la pressione in pascal, VM il volume della mole in m3, C una costante universale ed f (t) una funzione della temperatura espressa ad esempio in gradi centigradi, t. Se manteniamo costante il volume VM, la relazione 3) fornisce, per una temperatura prefissata t0 ed una temperatura variabile t: 4) p(t0)VM = C f(t0) 5) p(t) VM = C f(t) e dividendo membro a membro: 6) p(t)/P(t0) = f(t)/f(t0) => p(t) = p(t0)/f(t0)f(t) cioè 6’) p(t) = k0 f(t), con k0 = costante. e la pressione è proporzionale ad una funzione definita della sola temperatura. I rilievi sperimentali ottenuti misurando la pressione di un gas mantenuto in un volume costante al variare della temperatura dimostrano che la f(t) è lineare con la temperatura t, cioè è una funzione del tipo: f = at + b. Con ciò la 3) diventa : 7) PVM = C (at + b) = C a (t + b C/a) La stessa cosa avviene per il volume della mole qualora sia mantenuta costante la sola pressione. Assumendo t+bC/a come nuova espressione della temperatura e denominandola T (temperatura assoluta espressa in gradi Kelvin, K ) e ponendo C a = R si ha la classica formula dovuta a E. Clapeyron 8) pVM= RT dove b C/a risulta pari a 273,15 da cui T = t + 273,15 e Ca = R assume il valore di 8,31 J/mol K Questa formula è detta equazione dei gas perfetti. La 8) diventa per n moli di gas 9) pV = n RT, dove V = volume totale del gas Nel XIX secolo R. Clasius e J.C. Maxwell hanno elaborata una teoria statistica dei gas perfetti che ha permesso di correlare la temperatura assoluta T di un gas alla velocità quadratica media vm delle sue particelle. Si è trovato, nel caso di una mole di gas costituito da molecole monoatomiche che : 10) pVM = N m vm2 /3, dove : N = numero di Avogadro = numero di molecole costituenti la mole = 6,022 10 23 m = massa della molecola <v2> = media del quadrato delle velocità vm = (<v2>)1/2 = velocità quadratica media Da cui, l’energia cinetica media 11) <E> = m vm2 /2 =3RT/2N = 3/2 KB T Con KB costante di Boltzmannn = R/N = 1,38 10-23 J/K Cioè la temperatura T è direttamente proporzionale all’energia cinetica media delle molecole. Dalla equazione dei gas perfetti si vede che anche la pressione è proporzionale alla stessa energia cinetica. Se il gas è costituito da molecole non monoatomiche si ha: 12) <E> = f/2 KBT dove f = 3+n con n = numero di atomi costituenti la molecola, rappresenta il numero di gradi di libertà della molecola stessa. In fisica atomica come in chimica è usuale usare come unità di misura dell’energia l’elettronvolt eV. Per definizione rappresenta l’energia cinetica che assume un elettrone che passi attraverso la differenza di potenziale di un volt (V). La carica di un elettrone Q è pari a 1,602 10 –19 coulomb (C), l’energia corrispondente, VQ, è dunque pari a 1,602 10 –19 joule (J). Sostituendo tale valore nella 11) e ricavando T, si ottiene che 1 eV di energia cinetica media delle molecole monoatomiche di un gas equivale ad una temperatura di ca 7739 K. Rendimento termodinamico Molto importante è un’altra definizione della temperatura assoluta. Il rendimento
13) dove: L = lavoro prodotto Q1 = calore assorbito dalla
sorgente a temperatura t1 Q2 = calore rilasciato alla
sorgente a temperatura t2 Risulta, se t è espresso nella scala centigrada, f(t) = t + 273,15 da cui ponendo T = f(t) = t+273,15 si ha : 14)
15) Q1/T1 – Q2/T2 = 0 Il rendimento è = 1 solo se la temperatura della sorgente più fredda espressa nella nuova scala termodinamica è pari a 0 K. Tutte le macchine reversibili, cioè che operano attraverso dei cicli che avvengono mediante successivi stati di equilibrio e che utilizzano due sorgenti a temperatura T1 e T2, hanno lo stesso rendimento dato dalla 12), rendimento che si può determinare direttamente dal ciclo di Carnot dei gas perfetti. In tutti i casi reali, che sono irreversibili, il rendimento è sempre inferiore. L’identità dei rendimenti di tutti i cicli reversibili che avvengono tra due determinate temperature deriva dal 2° secondo principio della termodinamica una cui formulazione (dovuta a lord Kelvin) stabilisce che: E impossibile realizzare una macchina ciclica che produca lavoro utilizzando una sola sorgente di calore (impossibilità del motore perpetuo di seconda specie). Se ciò fosse possibile si potrebbe per attrito trasferire il lavoro, trasformato in calore, ad una sorgente a temperatura più alta, violando così l’altra formulazione del 2° principio (dovuta a R. Clausius) : Non è possibile trovare un dispositivo che faccia passare del calore da una sorgente ad una determinata temperatura ad una posta ad una temperatura superiore, avendo ripristinato alla fine le sue esatte condizioni iniziali
Dal secondo
principio nasce il concetto di entropia, indicata usualmente con S, introdotto
anch’esso da Clausius, variabile di stato, cioè legata solo ai parametri termodinamici e chimici del
sistema, la cui variazione per quanto concerne l’assorbimento di calore ad una
data temperatura T è data da Si è potuto dimostrare che per un sistema chiuso ed isolato cioè senza scambio di materia ed energia con l’ambiente : 16) S = KB logW Dove: KB = Costante di Boltzmann W = Numero degli stati microscopici (velocità , posizione, .. , di tutte le molecole) compatibili con lo stato termodinamico del corpo L’entropia aumenta sempre nell’universo ed è, in un certo senso, conseguenza della freccia del tempo. Irraggiamento del corpo
nero
Ogni corpo alla temperatura T > 0 irradia energia elettromagnetica . La radiazione totale per unita di superficie di un corpo ideale che assorba tutte le lunghezze d’onda (corpo nero) è data dalla formula di Stefan – Boltzmann 12) M = sT4 (W/m2) dove s è una costante indipendente dal corpo e dalla temperatura L’irraggiamento ha un massimo di emissione per una lunghezza d’onda inversamente proporzionale temperatura assoluta T (legge di Wien) 13)
c = costante Lo spettro di emissione (emissione specifica M per unità di frequenza) è dato dalla celebre formula di Planck 14) M( dove:
c = velocità della luce (m/s) h = costante di Planck (J) KB = costante di Boltzmann (J/kg) Attraverso l’irraggiamento si può definire ancora la temperatura assoluta T. Temperatura e
Cosmologia
Come è noto da Einstein la materia si può trasformare in
energia e viceversa, per cui nei primissimi istanti l’energia specifica, cioè
la temperatura era così elevata che esisteva un equilibrio termodinamico tanto tra l’energia dei fotoni data da
h Piccole variazioni, inferiori ad una parte su 100000, sono state notate dal satellite COBE (Cosmic Background Explorer) lanciato nel 1989 per studiare tale radiazione. Esse sono testimonianze di leggere disuniformità della temperatura e della densità del plasma primigenio, disuniformità che hanno ritardato localmente la ricomposizione elettronica modificando leggermente l’attuale spostamento verso il rosso. Tale disuniformità potrebbero aver dato origine, localmente, a contrazioni gravitazionali del gas cosmico mettendo in moto il processo che ha portato alla formazione delle galassie. Nel prossimo numero: Misura della temperatura Temperature dei corpi celesti Temperature dell’atmosfera terrestre |
 Il modello attualmente più accreditato di cosmogenesi è
quello del “Big Bang”. L’universo all’origine era tutto
Il modello attualmente più accreditato di cosmogenesi è
quello del “Big Bang”. L’universo all’origine era tutto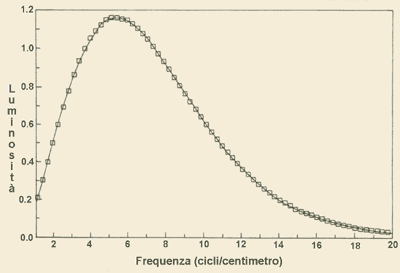 corrisponde in modo perfetto a quella di un corpo nero alla temperatura di
circa 2,72 K (fig. a fianco). Essa costituisce l’ immagine
corrisponde in modo perfetto a quella di un corpo nero alla temperatura di
circa 2,72 K (fig. a fianco). Essa costituisce l’ immagine