Temperatura, temperature, température, Temperatur
   di Diego Rosa

(quinta parte)

Le temperature termodinamiche

Fondamentale per la previsione del tempo è la conoscenza dello stato termodinamico delle masse d’aria: temperatura, pressione ed umidità in ogni loro punto. Tali grandezze variano con uno spostamento qualsiasi in direzione orizzontale e con la quota. Alcune funzioni della temperatura che tengono conto della quota e/o dell’umidità della particella sono più costanti in seno ad una medesima massa d’aria (aria che ha subito una determinata storia evolutiva nel corso dei suoi spostamenti e soggiorni nelle varie aree geografiche).Tali funzione più “conservative” vengono designate comunemente temperature termodinamiche e saranno brevemente descritte qui di seguito adottando sostanzialmente la terminologia di Hushke nel suo “Glossary of Meteorology” edito in Boston nel 1959 e ripresa da Pierre Pédelaborde nel suo “Introduction à l’étude scientifique du climat”edito da SEDES - Parigi nel 1982.
Le temperature termodinamiche sono ricavabili rigorosamente da formule matematiche ma si possono anche determinare dai diagrammi dei sondaggi aerologici (“émagrammes” nella letteratura francese).

Figura 1- Temperature termodinamiche nel diagramma aerologico obliquo

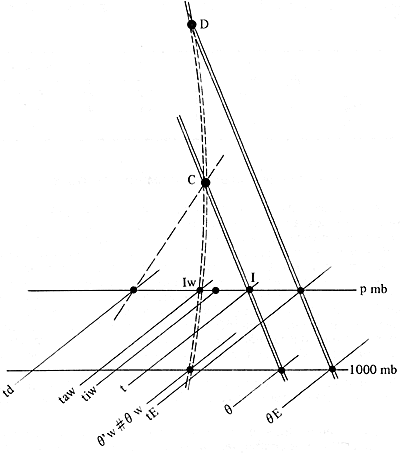
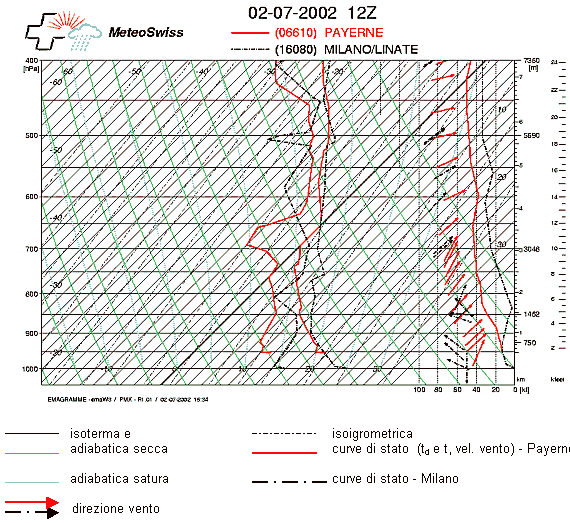
Fig 2 - Diagrammi aerologici del 2/7/2002, ore 12 UTC, di Payerne e Milano forniti da MeteoSwiss

Tali diagrammi ottenuti mediante radiosondaggi, sono normalmente del tipo detto “Skew T-ln p” con le coordinate verticali della pressione in scala logaritmica e le isoterme inclinate (skewed) sulla destra di 45°. Nelli stessi grafici sono tracciate normalmente le adiabatiche secche, le adiabatiche sature e le isoigrometriche cioè le linee che uniscono i punti aventi uguale rapporto di mescolanza di saturazione “ws” espresso in grammi di vapore per Kg di aria secca in saturazione. Il rapporto di mescolanza “w”, con il pedice “s” per indicare l’eventuale stato di saturazione, è praticamente uguale all’umidità specifica “q” espressa in grammi di vapore per Kg di aria umida.

L’utilizzo di isoterme inclinate consente di sfruttare meglio le dimensioni dei fogli ove tali grafici sono rappresentati e l’andamento normale della temperatura in un radiosondaggio si sviluppa secondo un andamento pressoché verticale; la scala logaritmica per le pressioni d’altro canto permette di misurare sullo stesso diagramma l’energia per unità di massa che una particella d’aria soggetta alla gravità ed alla forza di galleggiamento idrostatico assorbe o produce compiendo un sollevamento qualunque. Tale energia, la cui conoscenza è fondamentale per conoscere lo stato di stabilità od instabilità dell’atmosfera, è proporzionale all’area compresa tra la curva di stato e l’adiabatica che la particella segue nel sollevamento.

Nei diagrammi aerologici lo stato di una particella è rappresentato da un punto le cui coordinate sono temperatura e pressione. La pressione consente di determinare con sufficiente approssimazione la quota z riferendosi alla relazione p - z dell’atmosfera standard. L’umidità relativa (in percentuale di quella di saturazione a quella pressione ed a quella quota) può essere rappresentata o indicando direttamente accanto ad ogni punto il suo valore o più comunemente associando al primo un secondo grafico riportante o la temperatura del punto di rugiada td ( come nell’esempio di fig 2 –linea a sinistra di quella rappresentante la temperatura t) o la temperatura di bulbo bagnato tw , due temperature termodinamiche che descriviamo qui sotto.

Con riferimento alla figura 1 una particella d’aria è rappresentata dal punto I . Facendo subire a tale particella delle particolari trasformazioni otterremo le temperature termodinamiche:

Le temperature di bulbo bagnato (taw, tiw, uw)

- La temperatura adiabatica di bulbo bagnato taw si ottiene portando la particella adiabaticamente sino al punto C (punto di Rossby), iterazione della sua adiabatica secca con l’ isoigrometrica corrispondente al suo rapporto di mescolanza iniziale, “w”, e di qui, mantenendola satura riportandola alla pressione iniziale. Nota taw, è agevole determinare l’umidità relativa (rapporto della sua umidità specifica attuale con quella che provocherebbe la sua saturazione): essa è data semplicemente dal rapporto dei valori parametrici delle isoigrometriche passanti rispettivamente per C e per I ; C è ottenuto intersecando l’adiabatica secca passante per il punto I di temperatura t con quella satura passante per il punto Iw di temperatura taw.

- La temperatura isobarica di bulbo bagnato tiw è quella data dal bulbo bagnato dello psicrometro.

E’ facile mediante considerazioni di bilancio termico, determinare il rapporto di mescolanza o l’umidità specifica data la temperatura del bulbo secco t e quella di bulbo bagnato tiw :

Passando da t a tiw 1 kg di aria umida perde 0,24*(t- tiw) Kcal essendo 0,24 il calore specifico a pressione costante dell’aria secca corrispondente con ottima approssimazione a quello corrispondente dell’aria umida perché la massa di vapore in un Kg di aria secca è molto piccola ed il calore specifico del vapore non differisce molto da quello della stessa aria secca. D’altro canto saturandosi l’ aria assorbe 0,6*(ws- w) kcal, essendo 0,6 il calore di vaporizzazione dell’acqua (in kcal/g), ws il rapporto di mescolanza di saturazione alla temperatura tiw, w quello iniziale dell’aria alla temperatura t.

All’equilibrio si ha così:

0,6*(ws-w) = 0,24*(t- tiw)

cioè

ws- w = 0,4* (t- tiw) e w =ws-0,4*(t- tiw)

ws si legge sul diagramma aerologico per la temperatura tiw e la pressione p ( parametro dell’isoigrometrica per quel punto) o si determina mediante una formula analitica.
Nella pratica meteorologica tiw e taw differendo da 1 a 2 decimi di grado si confondono e dalla lettura dello psicrometro di tiw ~ taw si può determinare graficamente, come visto sopra, l’umidità relativa.

- La temperatura pseudo - adiabatica potenziale di bulbo bagnato u’w è ottenuta riportando la particella costantemente saturata (con temperatura iniziale taw) sino al livello di 1000 mb, mentre la temperatura adiabatica potenziale di bulbo bagnato w è ottenuta mediante la stessa trasformazione partendo però da tiw

La temperatura ’w si pres  ta particolarmente a contrassegnare una massa d’aria: si ha così sovente in inverno, in Europa occidentale:

- Aria artica marittima: Am ’w= 2 C°
- Aria polare marittima: Pm ’w = 3 C°
- Aria polare continentale: Pc ’w = -7 C°
- Aria tropicale marittima: Tm ’w = 9 C°

Le temperature equivalenti (tE , E)

Sono le temperature ottenute disseccando completamente la particella mediante una sua elevazione sino al punto C lungo l’adiabatica secca, indi lungo l’adiabatica satura. Discendendo in seguito lungo l’adiabatica secca sino alla quota di partenza si ottiene la temperatura adiabatica equivalente taE o semplicemente temperatura equivalente tE, proseguendo invece sino al livello di 1000 mb si ottiene la temperatura potenziale equivalente E.

La temperatura equivalente tE si deduce facilmente mediante le stesse considerazioni di bilancio termico fatte per la temperatura di bulbo bagnato.

Si ha indicando ancora con w il rapporto di mescolanza in g di vapore per kg d’aria secca:

w-0 = 0,4*(tE –t) da cui:

tE = t+ 2,5* w

Le temperature potenziali (, E , ’w, w)

Le temperature E , w, w sono già state trattate precedentemente, è ottenuta portando la particella d’aria, avente la temperatura t, al livello di 1000 mb secondo l’adiabatica secca.
Una relazione approssimata tra t e nella bassa e media tropopausa è la seguente:

= t+10*z con z = quota della particella in Km

Le temperature isobare (tiw, tE, td)

Sono le temperature che si riferiscono a particelle soggette alla stessa pressione del punto I. Di tiw e tE abbiamo già parlato, soffermiamoci ora su td la temperatura di rugiada, dew - point temperature in lingua inglese, température du point de rosée in lingua francese. Essa è la temperatura alla quale l’umidità presente nell’aria comincerebbe a condensare. E’ una funzione univoca della quantità di vapore presente nell’unità di volume (densità) e da ciò anche della pressione parziale del vapore stesso, pressione deducibile dalla densità mediante l’equazione di stato. Nei diagrammi aerologici l’intersezione della curva delle temperature di rugiada con una determinata isobara individua la curva isoigrometrica passante per quel punto; il rapporto del valore di mescolamento che le compete con quello relativo alla isoigrometrica passante per il punto dove la curva di stato incontra la medesima isobara, definisce l’umidità relativa “h” di quel medesimo punto. Le curve isoigrometriche incontrano le isoterme a temperature via via inferiori con la quota poiché con il diminuire della pressione l’umidità assoluta (g di vapore per m3 ) di una massa d’aria che si espande spostandosi verso l’alto, diminuisce (contrariamente al rapporto di mescolanza, g di vapore per kg di aria secca, che rimane costante) diminuendo in tal modo la temperatura che determina la sua saturazione.