Seconda parte

Descrizione dei risultati ottenuti

Esame critico delle caratteristiche

Nella Tab. 3 seguente sono riassunti i risultati sperimentali relativi agli strumenti oggetto dello studio dopo gli opportuni interventi di pulizia e regolazioni.

Tab. 3 – Risultati sperimentali
(*) valore medio fra tutti gli strumenti esaminati
(**) modello non confrontabile

Nella successiva Tab. 4 sono riportati gli intervalli di oscillazione dei parametri * e * medi per i soli strumenti modello SIAP per cui è stato possibile effettuare una taratura anche prima della completa pulizia.

Tab. 4 – Risultati sperimentali per il solo modello SIAP

Alcune cinsiderazioni sui modelli SIAP e LASTEM

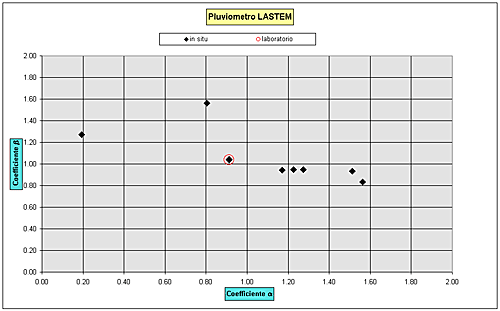
Per i modelli SIAP, è stato possibile effettuare dei controlli in situ e, successivamente, si è potuto effettuare una taratura dopo una completa pulizia in laboratorio, mentre per i modelli LASTEM si è operato attraverso il solo controllo in situ. Nel grafico di fig.3 sono riportati i parametri sperimentalmente ricavati per i pluviometri modello LASTEM che presentano, rispetto al modello campione, una ampia variabilità imputabile prevalentemente ad una mancanza di manutenzione e controllo. 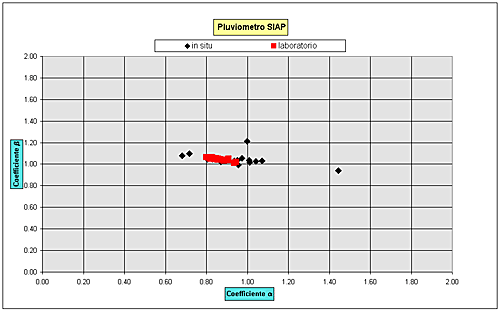La fig.4, relativa invece ai valori sperimentali ottenuti sui modelli SIAP, rappresenta in modo evidente l’efficacia dell’intervento di manutenzione che ha consentito di riportare i valori medi dei parametri e , nell’intorno di quelli medi originari e quindi riposizionare gli strumenti esaminati nel punto di taratura dichiarato dal costruttore (valore dell’intensità di pioggia a cui corrisponde un’errore percentuale certificato). L’ effetto di dispersione dei dati è dovuto all’impossibilità pratica di quantificare perfettamente l’acqua di scarico dopo il basculamento.

Fig.3 – Parametri sperimentali per pluviometri LASTEM

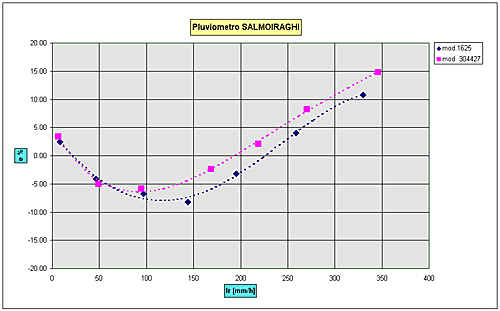
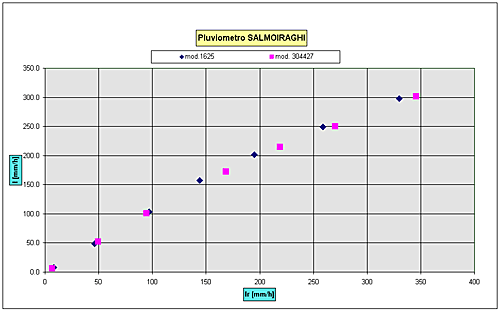
Fig.4 – Parametri sperimentali per pluviometri SIAP

Il pluviometro Salmoiraghi

I pluviometri modello Salmoiraghi presentano un singolare comportamento dinamico rispetto ai modelli esaminati sinora tale da non poter esprimere la curva di taratura attraverso l’equazione (1) in tutto il campo di funzionamento. Come infatti si può notare osservando i grafici delle figure 5 e 6 che seguono, ottenuti sulla base dei soli due modelli esaminati, per le basse intensità di pioggia si ha un comportamento simile agli altri modelli in cui l’errore aumenta all’aumentare dell’intensità di pioggia. Nel caso invece di piogge medioalte si ha un marcato recupero dell’errore.

Fig.5 – Curve di taratura dei pluviometri SALMOIRAGHI

Fig.6 – Curve di errore dei pluviometri SALMOIRAGHI

Questa tipologia di strumenti rientra comunque nella classe di pluviometri a bascula meritatamente alla tecnica di misura della pioggia sebbene la conformazione della vaschetta ed il meccanismo di riempimento non siano assimilabili agli altri pluviometri esaminati. Essendo questi strumenti non molto diffusi sul territorio preso in considerazione dagli autori, si è ritenuto rimandarne l’approfondimento successivamente.

Il pluviometro modello ETG

Il pluviometro modello E.T.G. rappresenta un classico strumento a bascula avente però la singolare caratteristica, unica fra tutti quelli esaminati, di associare ad ogni scatto della vaschetta, un valore di pioggia corretto in funzione dell’intensità. Dall’analisi fatta, è emerso che tale correzione non tiene conto però della reale curva di taratura dello strumento. Le figg. 7 e 8 rappresentano la curva di taratura e dell’errore rilevate in laboratorio.

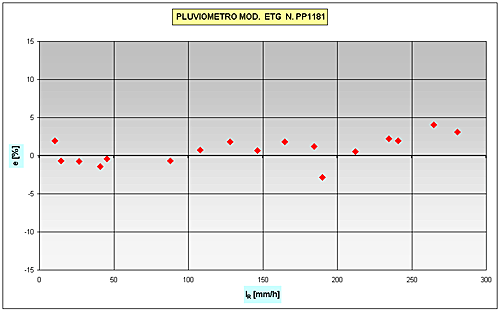
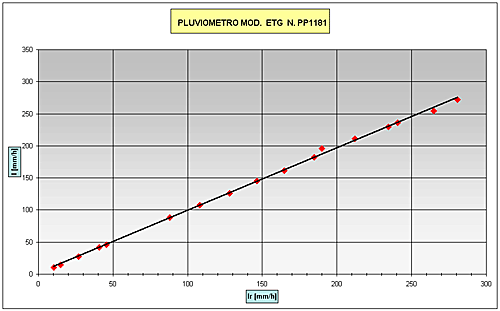
Fig.7 – Curve di taratura dei pluviometri ETG

Fig.8 – Curve di errore dei pluviometri ETG

In particolare, la curva di correzione dell’errore è assunta di tipo lineare definita secondo una retta passante per i punti I=0 mm/h (cui corrisponde un errore nullo) ed I=120 mm/h (cui corrisponde, nello strumento esaminato, un valore sperimentalmente pari a circa il 15 % in meno del valore reale). La logica di correzione del dato è matematicamente “discreta” e prevede che ad ogni movimento della bascula, nell’ipotesi che l’intensità di pioggia tra due rovesciamenti consecutivi sia costante, venga calcolata la quantità di mm di pioggia persa tenendo conto della curva di correzione dell’errore.

Quando le iesime differenze, sommate progressivamente, concorrono a formare una quantità di pioggia di 0.2 mm, corrispondente ad una basculata unitaria, quest’ultimo valore è automaticamente sommato alla quantità di pioggia registrata sino a quel determinato istante.

Curva di taratura e curva dell'errore di tutti i modelli esaminati

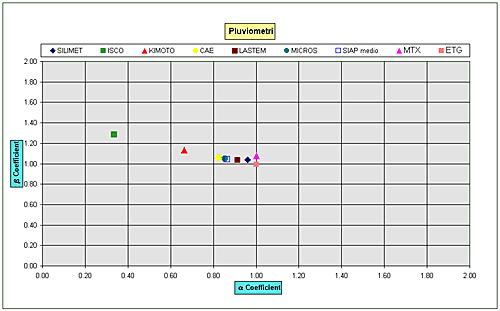
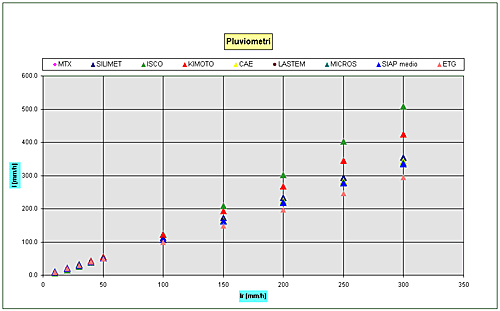
Nelle figure 9,10 e 11 sono riportate le curve di taratura espresse secondo le funzioni I/I_R e i parametri e , di errore in funzione dell’intensità di pioggia di tutti i modelli che sono stati esaminati.

Fig.9 – Parametri e di tutti i modelli esaminati

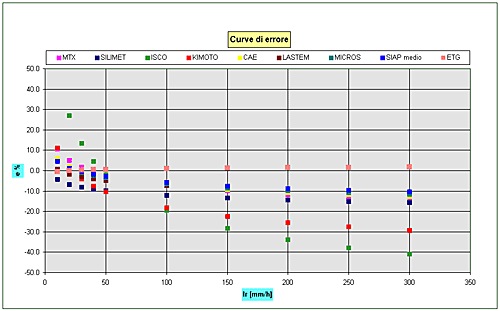
Fig.10 – Curve di errore di tutti i pluviometri esaminati

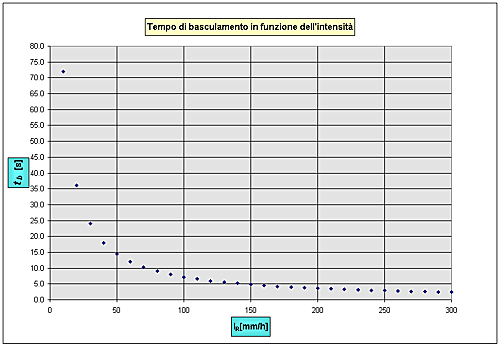
Fig.11 – Curve di taratura di tutti i pluviometri esaminati

Modalità di correzione dei dati di pioggia

Caso in cui sia nota la curva di taratura

In linea generale, se non si interviene dall’esterno con procedure apposite, i pluviometri a bascula sono strumenti il cui tempo di campionamento è variabile e la misura dell’intensità di pioggia caduta può essere effettuata solo successivamente al rovesciamento della vaschetta. Per poter procedere ad una correzione istantanea della pioggia caduta, si può intervenire di volta in volta attraverso i valori forniti dalla curva di taratura propria dello strumento sui valori da esso registrati nell’intervallo di tempo tb che intercorre tra due successivi rovesciamenti, nell’ipotesi che in tale intervallo l’intensità di pioggia rimanga costante. Nel caso in cui la strumentazione non sia in grado di fare ciò automaticamente, diventa fondamentale la scelta del parametro tc per eventuali correzioni a posteriori. Il grafico di fig. 12 riporta il valore di tb [s] in funzione di I[mm/h] consentendo di valutare l’intervallo di tempo tra due successivi basculamenti e quindi di determinare il numero di basculate possibili nel tempo tc scelto in funzione delle intensità di pioggia.

Fig.12 – Andamento di tc in funzione di I

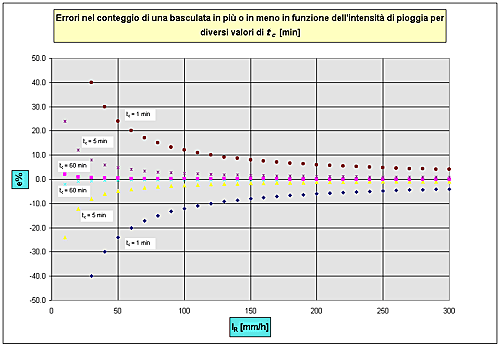
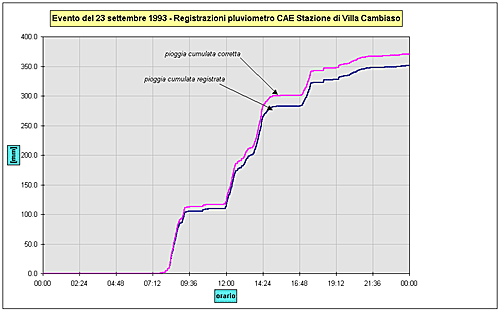
Fig.13 – Errori di conteggio delle bascule

Il grafico di fig.13 fornisce la stima dell’errore e% dovuto al conteggio di +/- una bascula in funzione dell’intensità di pioggia per alcuni valori di tc. Tale errore diminuisce all’aumentare di tc suggerendo, in prima analisi, l’adozione di tempi lunghi di acquisizione. L’aumento di tc, comporta che il valore assoluto dell’intensità diminuisca all’aumentare dell’intervallo di campionamento. Ne consegue che, per tutti i modelli esaminati, ad eccezione degli strumenti ETG e Salmoiraghi, una minore efficacia della correzione. Tale considerazione diventa di fondamentale importanza nella correzione e valutazione delle piogge nel campo di eventi pluviometrici particolarmente intensi. Dal momento che l’errore dovuto all’errato conteggio degli scatti può essere positivo o negativo compensandosi mentre l’errore dovuto alla correzione dell’intensità è sempre negativo, ne consegue che per minimizzare l’errore il tempo tc deve essere il più piccolo possibile. Quindi se tc = tb oltre ad eliminare l’errore dovuto al conteggio delle bascule quest’ultimo risulta essere ridotto al minimo. Nella Fig.14 vengono riportate a titolo di esempio le due curve cumulate, reale e corretta, nel caso di un evento particolarmente intenso.

Fig.14 – Curve cumulate evento del 23.09.1993 - Stazione di Villa Cambiaso - Genova

Correzioni secondo la classe degli strumenti

Una volta individuata la classe d’appartenenza dello strumento è possibile operare come segue:

Classe I: per questa classe di pluviometri è possibile una correzione a posteriori con l’ipotesi che l’intensità di pioggia rimanga costante durante il tempo di campionamento tc.

Classe II: anche questi strumenti permettono una correzione della pioggia a posteriori sebbene più efficace della Classe I. Infatti, si ha la possibilità di conoscere il tempo ti d’ogni basculata e quindi per differenza il tempo tb. In questo caso la correzione consiste nel modificare la Ir con la curva di taratura dinamica per ogni basculamento nell’ipotesi che l’intensità di pioggia rimanga costante durante il tempo tb intercorso tra due rovesciamenti. Particolare attenzione bisogna porre nella misura dell’intervallo tra due rovesciamenti in quanto eccessive approssimazioni comportano errori non trascurabili soprattutto nella valutazione dell’intensità di pioggia nel caso di eventi intensi con conseguente errore di correzione.

Classe III: questa classe di strumenti, nell’ipotesi che l’intensità di pioggia rimanga costante tra due basculate successive, permette la correzione del dato di pioggia attraverso la curva di taratura dinamica tra due successivi rovesciamenti della vaschetta. Tale correzione può considerasi la massima ed efficace possibile per i pluviometri a bascula in commercio.

Conclusioni

Da quanto precedentemente esposto si perviene alle seguenti considerazioni e conclusioni:

• gli strumenti analizzati non sono risultati omogenei in quanto gli stessi presentano caratteristiche meccaniche e regolazioni difformi. Da ciò ne consegue che ciascuno strumento ha una propria curva di taratura caratteristica;

• dalle analisi effettuate sulla strumentazione “in situ”, gli strumenti, sono risultati nella maggior parte dei casi fuori taratura. Solo dopo aver effettuato una completa manutenzione e ritaratura in laboratorio, è stato possibile riportarli nelle condizioni originarie di funzionamento;

• nessuna delle case costruttrici la strumentazione esaminata ha fornito una curva completa di taratura dinamica dello strumento, ma soltanto uno o due valori puntuali di pioggia, corrispondenti ad errori noti, che sono stati assunti come riferimento per la taratura dinamica;

• dal momento che lo studio era finalizzato alla valutazione delle piogge nel caso di eventi estremi, la mancanza di una curva di taratura non permette di valutare correttamente la pioggia caduta e registrata dallo strumento soprattutto nel campo di alti valori dell’intensità di pioggia.

• gli strumenti, ad eccezione del Salmoirgahi e ETG, presentano un errore che aumenta all’aumentare dell’intensità di pioggia.

• Alla luce di quanto sopra specificato, si ha motivo di ritenere necessario quanto segue:

• ogni strumento nuovo uscito dalla fabbrica debba essere corredato della sua curva di taratura dinamica onde permettere una più corretta valutazione della pioggia reale da esso registrata durante un evento nonché un immediato riscontro del suo corretto funzionamento nel corso delle regolari operazioni di calibrazione e manutenzione generale;

• qualunque sia la classe dello strumento sono necessari interventi più o meno incisivi sul software dei sistemi di acquisizione per la correzione della pioggia registrata con la curva di taratura dinamica.

• per alcune tipologie di strumenti si ritiene opportuno rivedere la progettazione in modo tale da consentire una quantificazione più accurata dell’acqua di scarico utile alla più precisa valutazione dell’errore e correzione dello stesso attraverso le regolazioni previste.

Bibliografia

BECCHI, I. (1970). “Sulla possibilità di migliorare le misure pluviometriche”. Pubbl. Istituto di Idraulica Università di Genova.
CALDER, I.R. KIDD, A. (1978). “Note on the dynamic calibration of Tipping-Bucket gauges”.J. Hydrology 39, 383-386.
DA DEPPO, L. (1977). “Sugli errori sistematici dei pluviografi a bilancia”. Convegno sulle metodologie di acquisizione e apparecchiature per la misura delle grandezze idrologiche e marittime, Napoli.
MARSALEK, J. (1981). “Calibration of the tipping bucket raingage”. J. Hydrology 53, 343-354.
MAKSIMIVIC, C. RADOJKOVIC, M. (1986). “Urban Drainage Catchments”. Pergamon Press.
NIEMCZYNOWICZ, J. (1986). “The dynamic calibration of tipping-bucket raingauges”. Nordic Hydrol. 17, 203-214.
PAGLIARA, S. VITI, C. (1994). “Taratura dinamica di un sensore di precipitazione a vaschette basculanti”. Bollettino Geofisico , n.2 pp63-69
W.M.O.
STAGI, L. (1996), “Strumento per la generazione di portata costante”. Quaderni di Laboratorio dell’Istituto dell’Idraulica dell’Università di Genova. N.18
LOMBARDO, F. STAGI, L. (1997).“Dinamic calibration of rain gauges in order to check errors due to hevy rainrates”. Poster in Conference “Water in the Mediterranean” – Istambul Nov.97
C.N.R. "Manuale di riferimento per la Misura al suolo delle grandezze idrometeorologiche”.

RINGRAZIAMENTI
Si ringraziano per la preziosa collaborazione le sottoelencate Società, Enti ed Istituti che hanno fornito la loro strumentazione per le verifiche di cui al presente studio:

· Acquedotto di Savona
· AMGA di Genova
· CIMA di Savona
· Istituto di Idraulica Università di Genova
· ITIS di Savona
· LASTEM di Milano
· Servizio Idrografico e Mareografico di Genova
· USL di Savona