L'arcobaleno
    di Diego Rosa

    Seconda parte

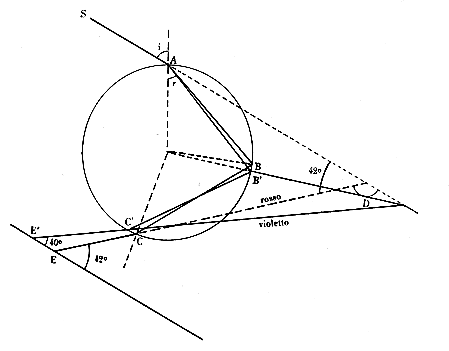
La teoria elementare dell’arcobaleno
(Descartes-Newton)

Una goccia sferica, si veda la Fig. 5, il cui centro si trovi su un piano passante per la retta congiungente l’osservatore con il centro del disco solare sia investita dal fascio di raggi paralleli del sole (trascuriamo le dimensioni angolari del sole pari a 0,5°).

Fig 5 Cammino dei raggi rossi e violetti, di minima deviazione, nella formazione dell’arcobaleno primario

Consideriamo il raggio generico S. Esso subisce in A una prima rifrazione ed entra nella goccia con un angolo r dato dalla relazione di Snell. Siccome l’indice di rifrazione dipende dal colore, le varie componenti della luce bianca costituenti il raggio, rifrangeranno con angoli diversi: così ad es. la componente rossa (la più rifratta) andrà in B, la violetta (la meno rifratta) in B’; le altre componenti in zona intermedia. In B e B’ i raggi subiranno oltre ad una rifrazione verso l’esterno, una riflessione interna che li manderà risp. in C e C’. Qui ancora una riflessione ed una rifrazione verso l’esterno, questa secondo le rette di traccia EC ed E’C’ con angoli rispetto alla direzione del raggio incidente diversi funzione dell’angolo di incidenza i.Tali angoli di deviazione totale per ogni colore od indice di rifrazione n presentano un minimo cui corrisponde un determinato angolo di incidenza i = im.Per il rosso ed il violetto esso è pari rispettivamente a circa 138° e 140° cui corrispondono gli angoli visuali E ed E’ di 42° e 40°, giusto le semi-aperture angolari degli archi rosso (il più esterno) e violetto (il più interno) rispetto all’asse sole-antisole. Per queste direzioni la luce rifratta avrà una luminosità massima. Tutte le gocce che si trovano sulla od in prossimità della retta che partendo dall’occhio dell’osservatore forma con l’asse sole-antisole uno degli angoli su indicati (ad es. ca 42° per il rosso) e giace sul piano considerato, contribuiranno, indipendentemente dalla loro distanza, a formare una porzione dell’immagine (virtuale) dell’arco.

Gli infiniti altri raggi deviati giacenti nel piano in esame, e caratterizzati da un angolo di incidenza diverso da im hanno una deviazione maggiore rispetto al raggio solare incidente. Ad essi corrisponde un’intensità della luce rifratta molto minore che viene a cadere o nei punti dell’immagine formati dai raggi di deviazione minima degli altri colori o all’interno del raggio di deviazione minima per l’incidenza ma massima per il colore (violetto), il per cui solo il rosso esterno dell’arco primario, di deviazione minima per il colore e per l’angolo di incidenza im, risulta abbastanza puro.

Avendo considerato un piano generico, per gli altri piani della stella avente come sostegno la retta congiungente il (centro) del sole con l’occhio dell’osservatore si possono fare considerazioni identiche. I raggi su di essi analoghi a quelli esaminati saranno le generatrici dei coni di luce di varia apertura al vertice e vario colore, con centro l’occhio dell’osservatore ed asse la retta di sostegno. Tali coni formano l’immagine completa dell’arcobaleno. 

Ricerca della deviazione minima

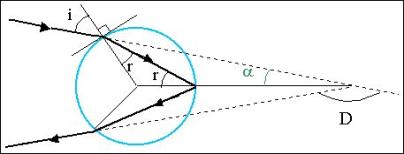
Fig. 6 Arco primario. Deviazione del raggio luminoso

Da semplici considerazioni geometriche l’angolo di deviazione D (valutato positivamente in senso orario tra il raggio incidente e quello deviato) risulta essere:

1) D = 180+2i-4r

La legge di Snell- Descartes dà:

2) sin(i) = n . sin(r);

con n = indice di rifrazione dell’acqua rispetto all’aria

da cui:

3) r = arcsin (sin(i)/n)

Differenziando la 2) si ottiene

4) dr/di = cos(i)/n.cos(r)

Deriviamo ora la 1) per trovare il minimo della deviazione D rispetto ad una variazione spessore del fascio incidente I (parametro d’impatto) valutato rispetto all’asse della goccia parallelo alla direzione del raggio incidente)

Ora è I =R.sin(i) con R = raggio della goccia e si ha semplicemente :

5) dI = d(Rsin(i)) = R.d(sin(i)) = R.cos(i).di

da cui:

5) dD/dI = 1/R.(2-4.cos(i)/n.cos(r))/(di.cos(i)) 

Per avere il minimo poniamo tale derivata = 0

si ha (per cos(i)# 0):

5’) 2.cos(i) = n.cos(r), da cui 

5”) 2cos(i)= n.cos(arsin(sin(i)/n)) 

e tenendo conto che cos(i) = (1-(sin(i))² )^0,5 e che sin(arcsin(x)) = x

6) 2cos(i) = n.(1-(sin(arcsin(sin(i)/n))²)^0,5 = n.(1-(sin(i)/n)²)^0,5

Elevando al quadrato:

7) 4.(1- sin²(i)) = n.(1-sin²(i)/n²) da cui:

8) sin²(i) = (4-n²)/3 e 

9) sin(i) = sin(i_m) = ((4-n²)/3)^0,5 

che conduce al valore dell’angolo di incidenza im che provoca la deviazione minima:

10) i = i_m = arcsin((4-n²)/3)^0,5

Ancora dalla 3) 

11) r = r_m = arcsin (sin(i_m)/n) = arcsin((4-n²)/3.n²)^0,5

Sostituendo i_m e r_m in 1), la deviazione minima D_m funzione del solo indice di rifrazione n, è data da:

12) D_m = 180+2. arcsin((4-n²)/3)^0,5 - 4.arcsin((4-n²)/3.n²)^0,5 

Al variare di i attorno ad im ed al parametro d’impatto Im= R.sin(im) fornito da dD/dI = 0, l’angolo dei raggi deviati resta sensibilmente costante.Ciò corrisponde ad un loro “addensamento”, rispetto a quelli paralleli entranti che gli hanno generati in questa direzione.Ciò porta ad una accresciuta energia luminosa in quella direzione.

L’indice di rifrazione n è legato alla lunghezza d’onda della luce l, dalla relazione di Cauchy:

13) n = n₀ + k/l² 

con n0 e k due costanti

si ha così n = 1,332 per il rosso (l = 780 nanometri) e n = 1,345 per il violetto (l = 430 nanometri) cui corrispondono risp. 2 angoli D_m pari 137,78° (angolo visuale 42,22°) e 139,64 (angolo visuale 40,36°). Lo spessore angolare dell’arco risulta così di 1,86°, 2,86° aggiungendovi il diametro angolare del sole.

Che la deviazione D aumenti continuamente con n si vede subito derivando D_m rispetto ad n

14) d(D_m)/dn = 2/n.((4-n²)/(n²-1))^0,5

e constatando come la derivata rimanga sempre positiva per ogni n > 0.

Arco secondario

Per l’arco secondario si possono fare considerazioni analoghe.

Esso è generato dai raggi che all’interno della goccia hanno subito una seconda riflessione (Fig. 5). 

Si ha in questo caso da semplici considerazioni geometriche:

15) D =6r-2i da cui

16) D = 6.arcsin(sin(i)/n) – 2.i

e cercando come prima il minimo di D si ottiene:

17) 3.cos(i) = n.cos(r)

che porge per l’angolo di incidenza di deviazione minima im:

18) i_m = arcsin((9-n²)/8)^0,5

da cui

19) D_m = 6. arcsin((9-n²)/8.n²)^0,5 – 2. arcsin((9-n²)/8)^0,5

Al contrario che nell’arco primario qui la derivata di D_m rispetto ad n:

20) d(D_m)/dn = -2/n.((9-n²)/(n² –1))

è sempre negativa per cui Dm diminuisce all’aumentare di n ed il violetto (angolo visuale 53,99°) si troverà all’esterno, il rosso (angolo visuale 50,63°) all’interno.

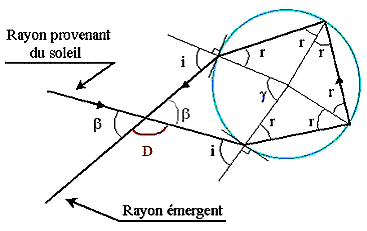
Fig. 7 Arco secondario. Deviazione del raggio luminoso

La Teoria di Young-Airy

La teoria elementare su esposta non spiega la formazione degli archi soprannumerari, del colore sbiadito e della diversa dimensione degli archi delle nebbie piovigginose e delle nuvole.

Secondo la teoria di Young completata da Airy questi fenomeni sono dovuti all’interferenza delle onde luminose all’interno delle gocce d’acqua. Essa provoca effetti diversi in funzione del raggio R delle gocce.Tale raggio raramente supera i 2,5 mm con un valore medio di 0,5 mm per la pioggia, è attorno ai 0,1 mm per la pioviggine ed attorno ai 0,01 mm per le nuvole. 

Nelle gocce più piccole l’interferenza produrrà colori molto sfumati per la sovrapposizione di massimi minimi delle figure di interferenza. Solo con gocce abbastanza grosse l’arcobaleno assume l’aspetto previsto dalla teoria di Descartes-Newton. 

Ad esempio con gocce aventi R< di 0,3 mm il rosso non è più visibile; con gocce con R < di 0,025mm l’arcobaleno risulta di colore bianchiccio.

Gli archi soprannumerari

Gli archi soprannumerari, inizialmente bianchicci come l’arco principale cominciano a manifestarsi con R tra 0,02 e 0,01 mm e via via diventano sempre più fitti ed angolarmente meno spessi. I colori dell’arco primario appaiono con R >0,1 mm con il rosso sempre più vivido ai 42° visuali. Aumentando il raggio R tra 0,5 e 1 mm i sopranumerari diminuiscono di luminosità relativa piuttosto che in quella assoluta e l’arco assume l’aspetto famigliare con i canonici colori dell’iride.