|
Parte terza
Stabilità instabilità atmosferica
Introduzione alla termodinamica
Abbiamo visto che il primo principio
della termodinamica identifica una grandezza, l’energia
interna U, la cui variazione infinitesima durante un
processo termodinamico è data da
1)
dU =
δQ
–
δW
grandezza che è funzione dei valori dei
parametri che caratterizzano il sistema (ad es. per i gas
perfetti da due delle variabili:
P (pressione),V
(volume) , T
(temperatura assoluta) . Essa è una così detta funzione di
stato. Il calore scambiato infinitesimo
dQ ed il lavoro
prodotto dW
sono invece grandezze che si riconoscono solo nel mentre
transitano, il calore, o si realizzano, si applicano, il
lavoro. In termini matematici si dice che
dQ e
dW, che si
sogliono indicare in questo caso con
δQ e
δW, non sono in
generale, come si dice in analisi matematica, differenziali
esatti. Nel qual caso il loro integrale da uno stato
A ad uno stato
B del sistema
dipende sempre dal percorso (termodinamico) per andare da
A a
B, al contrario
della loro differenza,
dU, che integrata definisce in modo univoco quanto
cambia la funzione di stato
U.
La 1) per un sistema isolato
(δQ e δW = 0)
dà dU = 0 ,
l’energia interna di un sistema isolato si conserva.
L’energia interna
U della
relazione 1) è data dalla somma dell’energia cinetica e di
legame delle molecole o atomi del corpo.
Se consideriamo l’energia totale del
sistema in esame Ut
comprensiva :
- Della stessa energia interna
U
- Dell’ energia cinetica macroscopica se
il sistema è in movimento che è data approssimativamente da:
E = ½ m v2
con
m massa a
riposo e
v velocità ,
per velocità ordinarie, ma da :
E= ½ [m/(1- v2/c2)]v2
per velocità prossime a quella della luce
c (relazione
di Einstein per la massa in movimento)
-Dell’energia propria della massa a
riposo
m , ancora da
Einstein
Em = mc2
-Delle energie potenziali:
gravitazionali, elettrostatiche e magnetiche del sistema
abbiamo ancora per un sistema isolato e per l’universo
intero nella misura in cui possa essere considerato tale che
:
2)
ΔUt = 0
L’energia totale si conserva, non
può essere né creata né distrutta.
Mi tornano in mente i versi di Lucrezio,
seguace della filosofia atomista di Empedocle, Democrito ed
Epicuro, nel suo “De rerum natura” (Inno a Venere, libro
primo ): “Principim cuis hinc nobis exordia sumet: nullam
rem e nihilo gigui divinitus umquam”: “ Il cui principio
prenderà da noi l’avvio da questo: dal nulla non può nascere
nulla per principio divino”.
|

Fig.1 - Y. R. von Mayer 1814 - 1878
Heilborn - Germania. Fisico e biologo tedesco
|
|
Ancora a fine settecento il grande
Lavoisier (preceduto 50 anni prima dallo scienziato
scrittore ed astronomo russo Lomonosov) fondatore della
chimica quantitativa, affermò: “Nulla si crea, nulla si
distrugge. Tutto si trasforma”
Nel 1842 il fisico e medico tedesco J.
von Mayer nella pubblicazione di maggio degli “Annalen der
Chemie und Pharmacie” asserì non solo che il lavoro non può
sparire ma può trasformarsi in calore e ciò in base a
considerazioni e riflessioni maturate negli anni, dando pure
una valutazione sorprendentemente corretta dell’equivalente
meccanico del calore, valutazione che aveva ricavato dalla
differenza dei calori specifici dei gas a pressione rispetto
a quelli a volume costante:
CP - Cv
= R (costante dei gas perfetti in
PV= RT)
Tale affermazione passò sotto silenzio perché non supportata
da prove né da un formalismo matematico adeguato. Nel 1850
Joule che pure considerazioni analoghe aveva fatto anni
prima, condusse il celebre esperimento con cui determinò
direttamente, con grande accuratezza, l’equivalente
meccanico della caloria. Una lunga controversia nacque su a
chi attribuire tale scoperta a Mayer o a Joule.
Lo stesso Joule facendo espandere un gas
in un ambiente chiuso, rigido e termicamente isolato
verificò che la sua temperatura sensibilmente non cambiava .
Il lavoro compiuto dal sistema (aumento di volume del
sistema = 0 ) era nullo, il calore scambiato
(δQ = 0)
egualmente nullo. Si poteva dedurre che l’energia interna
U fosse
dipendente solo dalla temperatura,
U = U(t). Cioè
è vero in prima approssimazione per i gas a bassa pressione,
nei quali le forze di attrazione intermolecolare sono
trascurabili. Dunque si può considerare in questo caso:
3) dU =
dQ = df(T)
Con
df(T) = Cv dT
Dove
Cv
= calore specifico a volume costante
2. Trasformazioni
termodinamiche scaturenti dalla prima legge
Alcune trasformazioni termodinamiche sono
di particolare interesse:
1 -Trasformazione isoterma (la
temperatura rimane costante)
2 - Trasformazione adiabatica (senza
apporto di calore, il sistema è termicamente isolato)
3 - Trasformazione isocora (il volume
rimane costante)
4 -Trasformazione isobara (la pressione
rimane costante)
Trasformazione isoterma (per i gas perfetti)
Riprendiamo la relazione
dU = δQ – δW
Che per i gas in espansione possiamo
scrivere
δW= PdV (in
effetti il lavoro elementare è dato da una forza per uno
spostamento =
f ds ,
P è una forza
su una superficie unitaria
P = f/S e
dV può essere
inteso come una superficie
S per uno
spostamento da cui
dW = Pdv = (f/S) S ds = fds )
Il che porge essendo ipotizzando
U solo
funzione di
T per cui
dU(T) = 0
4) δQ –
PdV = 0
Per l’equazione dei gas perfetti
(riferendosi ad una mole) si ha:
PV = RT da cui
sostituendo
p in funzione
di
V, P = RT/V e
scrivendo
δQ =dQ (ora
l’aumento del calore assorbito
δQ = dQ
essendo solo funzione di
P e
V , variabili
i stato) abbiamo:
5) dQ = RTdV/V
questa è una semplice equazione
differenziale che integrata da:

Il calore scambiato è direttamente
proporzionale al logaritmo naturale del rapporto dei volumi,
inversamente proporzionale al rapporto del logaritmo
naturale delle pressioni.
|
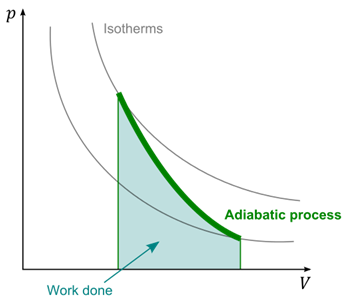
Fig. 2 - Trasformazioni isoterme ed adiabatica
per un gas perfetto
|
|
|
Trasformazione adiabatica
Per una trasformazione adiabatica vale la
relazione:
7) dU = PdV
Essendo nullo il trasferimento di calore
δQ
Ora abbiamo
dU = Cv dT
e come sempre
P = RT/V da
cui:
8) Cv dT = RTdV/V
Ed ancora:
9) Cv/R dT/T = dV/V
che integrata da:
10) Cv/R
ln T = ln V + C, C
= costante che porge elevando i due membri
alla potenza di e:
11 ) T(Cv/R) = eC
V
12) T(Cv/R) /V = eC
= costante
dalla
PV= RT e
R = CP - Cv
con una semplice manipolazione ponendo
Cp/ Cv
= γ si ha anche:
13)TV γ-1 = costante
Ed ancora utilizzando la relazione
PV = RT:
14)
PV γ = costante
15) TP
(1-γ)/ γ = costante
Trasformazione isobara
Abbiamo:
16) δQ = dQ = dU+ PdV
con P costante
Derivando la
PV = RT si ha,
con
P costante,
PdV = RdT da
cui :
17) dQ = Cv dT + R
dT = (Cv+ R)dT da cui
18) dQ/dT = Cv +R
= CP
CP
è il calore specifico a pressione costante. E’ la
fondamentale relazione dovuta a Mayer per la determinazione
dell’equivalente meccanico del calore
Trasformazione Isocora
E’ la trasformazione che avviene a volume
costante.
Abbiamo ancora dalla
14) con
dV = 0
19) δQ =
dQ = dU = Cv dT
Il calore scambiato è pari all’aumento
dell’energia interna.
|