|
Parte quinta
Stabilità instabilità
atmosferica
Introduzione alla termodinamica
1) Entropia concetto
fondamentale nell’universo
Abbiamo visto che ogni trasformazione
fisica implicante il passaggio di calore e lavoro il valore
dato da
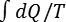 su un ciclo chiuso qualsiasi sia
su un ciclo chiuso qualsiasi sia
≤ 0 dove
dQ è la
quantità di calore ricevuta dal sistema e
T la
temperatura assoluta alla quale avviene lo scambio
infinitesimo.
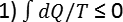
Se la trasformazione è reversibile nel
senso che la trasformazione può essere ricondotta allo stato
iniziale senza lasciare alcuna traccia nell’universo,
l’integrale è = 0 e dQ/T
può essere ritenuto il differenziale esatto
dS di un
grandezza S
variabile di stato cioè individuata solo dai parametri
fisici del sistema come ad esempio per i gas perfetti
P,V,T e
definita da Clausius come
S = Entropia.
La 1) definita su un ciclo tra
A e
B irreversibile
e tra B ed
A reversibile
porge (per la definizione di reversibilità)
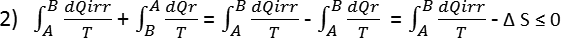
Da cui per una trasformazione qualsiasi:
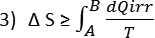
|

Fig. 1 - Ludwig Boltzman. Vienna 1844, Duino
1906. Uno dei più grandi Matematici e fisici
dell’ottocento
|
|
E se il sistema in cui avviene la
trasformazione è isolato,
dQ = 0 e Δ S ≥ 0.
L’entropia in un sistema isolato non può diminuire ma solo
aumentare. L’intero universo isolato per definizione
vedrebbe la sua entropia sempre aumentare.
L’entropia è anche associabile al grado
di disordine o meglio di omogeneizzazione di un sistema. Se
versiamo un po’ di caffè in un bicchiere di latte avremo un
a sua rapida omogeneizzazione in modo irreversibile e non
succederà mai il contrario . L’entropia del sistema è
aumentata.
Il grande Fisico e matematico austriaco
Ludwig Boltzman nel 1870 determinò la relazione che associa
l’entropia termodinamica di Clausius alla statistica del
grado di disordine o meglio di omogeneizzazione del sistema:
4)
S= -kB ln Ω
Dove
kB e una
costante pari a 1,38
10-23 J/K ed Ω
è il numero di microstati che determina una determinata
configurazione termodinamica espressa nel caso di un gas
ideale da P,V,T
L’aumento dell’entropia è dunque legata
logaritmo delle configurazioni che determinano un dato stato
termodinamico logaritmo che appare anche nella termodinamica
classica che porge, per un gas perfetto:
5)
S = Cvln T
+ R ln V + C
Con
Cv = calore specifico a volume costante
T = temperatura
assoluta
V = volume
R = costante
dei gas
I Buchi neri
|

Fig. 2 - Stephen Hawking. 8/11/1942 Oxford. Una
dei più grandi fisici , cosmologi e matematici
del nostro tempo. Membro della Royal Society
|
|
Evidenze astronomiche, la fisica
nucleare, la relatività generale di Albert Einstein fanno
ipotizzare una particolare evoluzione dei corpi celesti con
massa iniziale superiore a ca. 10 volte quella solare.
Esaurito il loro combustibile nucleare che alimentava le
reazioni di fusione, la forza di gravità non più bilanciata
dalla pressione interna li farebbe collassare verso il
proprio interno, verso un punto centrale teoricamente a
densità e gravità infinite. L’oggetto cosi ipotizzato
chiamato buco nero (black hole) conserverebbe solo tre
caratteristiche fisiche: la massa , la carica elettrica ed
il momento angolare. Attorno al buco nero esiterebbe uno
spazio caratterizzato dal raggio di Schwarschild otre il
quale ne materia né radiazione potrebbero uscire. La
velocità di fuga su quel raggio sarebbe infatti pari al
limite, invalicabile della velocità della luce, al suo
interno superiore, impedendo così ogni uscita di materia o
radiazione .
Ogni oggetto materiale, ogni radiazione
che oltrepassasse il raggio di Schwarschild verrebbero così
intrappolati e persi per sempre. Ma ogni oggetto trasporta
con se entropia che in tale modo verrebbe sottratta
definitivamente a quella totale dell’universo contravvenendo
al secondo principio della termodinamica. A fronte di tale
possibile paradosso Stefan Hawkings tenendo conto che nel
vuoto grazie al principio di indeterminazione di Heisemberg
si ha una continua produzione di particelle ed
antiparticelle che si annichilivano con continuità, ha
ipotizzato che quelle che varcano il confine di Schwarschild
(di massa negativa) vengano perse mentre le altre possano
sfuggire contribuendo così a una specie di evaporazione del
buco nero ed ad aumento dell’entropia dell’universo
conservando la validità del secondo principio.
|