|
Parte sesta
Stabilità instabilità
atmosferica
Abbiamo parlato nella parte precedente
dei buchi neri come residui iperdensi dell’evoluzione finale
di masse stellari maggiori di quella solare. La superficie
che in qualche modo li delimita, chiamata superficie di
Schwarzchild dal fisico e cosmologo Karl Schwarzchild che
per primo la definì, è quella dall’interno della quale
nessun oggetto né segnale elettromagnetico può sfuggire
perché trattenuto dalla gravità . Su di essa la velocità di
fuga è uguale alla insuperabile (Albert Einstein) velocità
della luce nel vuoto, ca 300000 Km al secondo.
|

Fig. 1 - Isaac Newton. Woolsthorpe 1642, Londra
1727.
Uno dei più grandi matematici e fisici della storia.
Fondò con Wilhein Leibniz il calcolo differenziale.
|
|
|
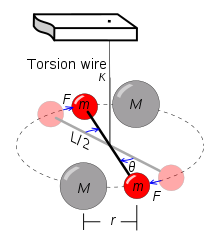
Fig. 2 - Schema meccanico dell’esperimento del
fisico e chimico scozzese Cavendisch
|
|
La velocità di fuga da un corpo di massa
m1 di un corpo di massa qualsivoglia si ricava
molto semplicemente.
La forza di attrazione di due masse m1
e m2 la cui distanza tra i rispettivi centri di
gravità è r, è data dalla celebre relazione di Newton
1)
F = G m1 m2/r2
Con G = costante di
gravitazione universale.
La forza F che
agisca su uno spostamento ds da un
lavoro dL , espresso in termini
differenziali da :
2)
dL
= F ds
Il fisico e chimico scozzese Cavendisch (Fig. 2) nel
1785 calcolò la densità della Terra e determinò la costante
G .
Dalla distanza r, dalla torsione
Θ , dalla lunghezza del braccio
L, dal coefficiente di torsione
k e dal peso delle masse
M ed m determinò
il coefficiente G mediante la
relazione:
FL =kΘL = LGMm/r2
Il lavoro della 1) dalla distanza
r all’infinito è dato dall’integrale :
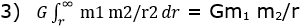
L’integrale pur avendo l’estremo
superiore infinito ha un valore finito e con esso il lavoro
per sconnettere il vincolo gravitazionale dei due corpi.
D’altro canto, dall’altra celebre
relazione di Newton
4) f = ma
che lega la forza f
alla massa m ed all’accelerazione a = dv/dt
del corpo e dalla definizione di lavoro
dl= f ds con ds =
spostamento infinitesimo = v dt si ha :
5) dL = m dv/dt ( v dt) =
m dv v
Che integrata da 0
a V da:
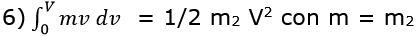
Questa e’ l’energia cinetica o forza viva
del corpo di massa m2 e velocità V.
Uguagliamo ora la 3) alla 6) abbiamo:
7) Gm1
m2/r
= 1/2 m2 V2 , Gm1
/r = 1/2 V2 , V = 2 (Gm1/r)1/2
V è la velocità di
fuga del corpo in questione ed è indipendente dalla sua
massa m2.
Chiediamoci ora, in modo puramente speculativo, a quale
valore dovrebbe ridursi il raggio della terra (ca 6000Km)
per diventare un buco nero.
La velocità di fuga sarebbe in questo caso pari alla
velocità della luce.
Abbiamo:
G= 6,67 10-11 m3/(Kg s2)
m1 = 5,97 1024 Kg
V = 3 108 m/s
La 7) da r =2Gm1/ V2
= 8,8 10-3 m
Un raggio inferiore al cm!
|
Fig. 3 - Jacob David Bekenstein
(Città del Messico, 1º maggio 1947 – Helsinki, 16
agosto 2015)
Ha contribuito alla fondazione della termodinamica
dei buchi neri e ad altri aspetti riguardanti la
connessione tra l'informazione e la gravitazione.
|
|
Ogni corpo che cadendo nel buco nero
oltrepassasse il raggio di Schwarzchild (delimitante il così
detto orizzonte degli eventi) recherebbe con sé la
struttura, le informazioni, il marchio della sua struttura
quantistica (ad esempio numero di barioni) ed un’entropia.
Se queste venissero perse per sempre si violerebbe da una
parte il fondamento della meccanica quantistica, dall’altra
la seconda legge della termodinamica che stabilisce che
l’entropia dell’universo non può mai diminuire. Da questi
fatti J. Bekestein congetturò che i buchi neri hanno
un’entropia proporzionale all’area dell’orizzonte degli
eventi, entropia che in seguito Hawking determinò essere
data dall’espressione:
8) S=KBA/4(lp)2
Con:
A =
area dell’orizzonte degli
eventi (m2)
Lp = lunghezza di Planck = 1,616
10-35 m
KB= Costante di Boltzman = 1,38
10-23 J/K
Che danno
9) S = 1,38 1046 A J/K
Valore immenso anche per il mini buco
nero “Terra” che con
A = 9,7 10-4 m2
da S
= 1,26 1043 J/K.
|